
Stochastic gradient descent, often abbreviated SGD, is a variation of the gradient descent algorithm that calculates the error and updates the model for each example in the training dataset.

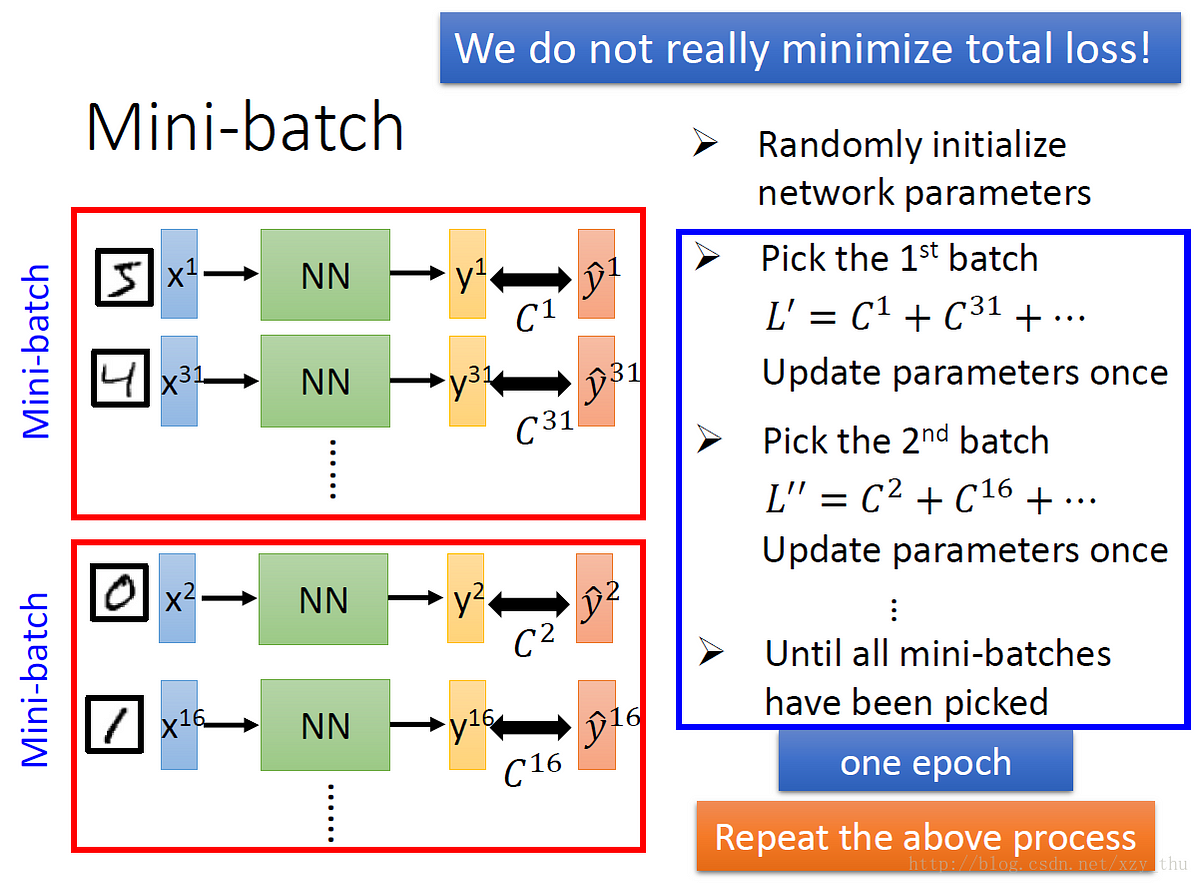
It is faster than the batch gradient descent.It is done because some hardware such as GPUs achieves better runtime with batch size as a power of 2. Generally, it is chosen as a power of 2, examples 32, 64, 128, etc. We divide our data set into several mini-batches say n batches with certain batch sizes. So even we have a large number of training examples, it is processed in batches of certain examples (batch size). In this algorithm, instead of going through entire examples (whole data set), we perform a gradient descent algorithm taking several mini-batches. It takes a long time to converge if we have large data set.

#BATCH GRADIENT DESCENT UPDATE#
In this algorithm, we consider all of our examples (whole data set) on each iteration when we update our parameters. It is also simply called gradient descent. Now let’s discuss in brief the variants of gradient descent algorithms. We continue this process until the cost function converges. We then update our previous weight wand bias b as shown below:Ħ. On each iteration, we take the partial derivative of cost function J(w,b) with respect to the parameters ( w,b):ĥ. Suppose our cost function/ loss function ( for brief about loss/cost functions visit here.) which is to be minimized be J(w,b). For their details about Normalization, you can visit this page.Ĥ. There are various techniques of normalization. The data should be normalized to a suitable scale if is highly varying. In the same way, if the value of the learning rate is too large, it will overshoot the minimum and fail to converge.ģ. If the learning rate is too small, it would take a long time to converge and thus will be computationally too expensive. the learning rate is a factor that determines how big or small the step should be on each iteration. Initialize our w and b with random guesses. For this the algorithm can be written as:ġ. For convenience, let’s suppose that our model has only two parameters: one weight w and bias b. For this let’s take an example of the logistic regression model. Gradient descent is also known as the steepest descent.īefore going through the variants of gradient descent let’s first understand how the gradient descent algorithm works. If, instead, one takes steps proportional to the positive of the gradient, one approaches a local maximum of that function the procedure is then known as gradient ascent. To find a local minimum of a function using gradient descent, one takes steps proportional to the negative of the gradient (or approximate gradient) of the function at the current point. Gradient descent is a first-order iterative optimization algorithm for finding the minimum of a function (commonly called loss/cost functions in machine learning and deep learning). But this can also be understood as SGD, provided the data stream is not containing some weird regularity.Introduction To Gradient descent algorithm (With Formula) Some people refer to online learning as "batch gradient descent", where they use, new batches from a datastream only once, and then throw it away. That's why it is called stochastic gradient descent (SGD).ĭoing "batch gradient descent" without any randomness in the choice of the batches is not recommended, it will usually lead to bad results. Now, most of the time, those batches are chosen via some kind of random procedure, and that makes the gradients that are computed at each step, random, i.e. Different batches result in different functions and thus different gradients at the same parameter vector. Thus, at each step, another function (different from the actual objective function (the loglikelihood in our case)) is taken to take the gradient of. There is nothing stochastic (random) about it.īatch gradient descent doesn't take all of your data, but rather at each step only some new randomly chosen subset (the "batch") of it. This is the most standard optimization procedure for continuous domain and range.
it is using, at each step, the actual function that is to be optimized, the loglikelihood. Gradient descent takes, at each iteration, all of your data to compute the maximum of your loglikelihood, i.e.


 0 kommentar(er)
0 kommentar(er)
